小學數學思維訓練“十佳題”(2)
1. 在□里填上不同的質數,使等式成立。□+□=□×□=□-□
【分析與解答】 如果兩個質數的和(或差)是奇數,那么必須是奇數與偶數的和(或差),而偶質數只有2,則填寫重復。所以這個和只能是偶數。一個因數是2.可以列出100以內的質數來選擇列舉。
3+7=2×5=23-13 3+11=2×7=37-23
3+7=2×5=71-61 3+19=2×11=29-7 ……
2.甲乙兩種奧運會紀念品的單價相差0.6元,用36元錢買乙種紀念品比買甲種紀念品剛好可以多買2個,則甲的單價是多少元,乙的單價是多少元?【分析與解答】 以角做單位,則
360=甲的單價×甲的數量=(甲的單價-6)×(甲的數量+2)。
360=1×360=2×180=…=10×36=12×30=15×24=18×20
觀察知道,甲的單價是36角,即3.6元,乙的單價是3元。
3.一個長方體的玻璃缸,長8分米,寬6分米,高4分米,水深2.8分米,如果投入一塊棱長為4分米的正方體鐵塊,缸里的水溢出多少升?
【分析與解答】 鐵塊的體積 4×4×4=64(立方分米)
水的體積 8×6×2.8=134.4 (立方分米)
玻璃缸的容積 8×6×4=192 (立方分米)
注意到鐵塊的高度與玻璃缸的高度相同,而水的體積與鐵塊的體積的和比玻璃缸的容積大,則溢出水的體積是 64+134.4-192=6.4 (立方分米)=6.4(升)
4.一個棱長10厘米的正方體的玻璃缸,水深3厘米,如果投入一塊棱長6厘米的正方體鐵塊,缸里的水上升了多少厘米?【分析與解答】正方體沒有淹沒于水中,所以不能用正方體的體積÷底面積.根據水的體積不變,而水的底面積由10×10=100(平方厘米)變成了(10×10-6×6)平方厘米了,由此可以求出水的高度.
10×10×3÷(10×10-6×6)=4.6875 (厘米)
上升 4.6875-3=1.6875 (厘米)
5.一個棱長10厘米的正方體的玻璃缸,水深4厘米,如果投入一塊棱長6厘米的正方體鐵塊,缸里的水上升了多少厘米?【分析與解答】開始好像正方體沒有沒于水中,如上計算水深是
10×10×4÷(10×10-6×6)=6.25 (厘米)
大于6厘米說明水已經淹沒了鐵塊,計算上升的高度直接用鐵塊的體積÷玻璃缸的底面積.
6×6×6÷(10×10)=2.16(厘米)
另解:當知道鐵塊沒于水中后,由水的體積也可求高度.鐵塊高6厘米,鐵塊周圍的水是以底面積是(10×10-6×6)平方厘米來計算的,高于鐵塊的部分的水的底面積是10×10=100平方厘米.
〔10×10×4-(10×10-6×6)×6〕÷(10×10)+6-4=2.16(厘米)
6.把數字1至9填入算式中,使等式成立。 □/□=□/□=□□/□□□
【分析與解答】 2/4=3/6=79/158 (填法很多)
7.把數字1至9填入算式中,使算式成立。 □□□□×□=□□□□
【分析與解答】1738×4=6952 或 1963×4=7852
8.在射箭比賽中,每射一箭得到的環數或者是“0”(脫靶),或者是不超過10的自然數,甲、乙兩名運動員各射了5箭,每人5箭得到的環數的積都是1764,但是甲的總環數比乙少4 環。求甲、乙的總環數。【分析與解答】因為每箭射中的環數都是1764的因數,而
1764=2×2×3×3×7×7,并且環數是不超過10的自然數。
所以必有兩箭是7環。其它3箭是2×2×3×3的因數,有5種可能:
7,7,1,4,9 和為28; 7,7,2,3,6 和為25;
7,7,1,6,6 和為27; 7,7,3,3,4 和為24;
7,7,2,2,9 和為27
因為甲的總環數比乙少4,所以甲的總環數是24,乙的總環數是28.
9.在算式1997÷□=□…9 的兩個方框中填入適當的數,可以組成正確的算式,這樣的算式共有多少個?【分析與解答】 1997-9=1988是除數的倍數,而除數大于余數9,也就是求1988的大于9的因數有多少個。列舉得到 :答案是8個
10.龜兔進行10000米賽跑,兔子的速度是烏龜的5倍,當它們從起點出發后,烏龜不停地跑,兔子跑到某一地點開始睡覺,兔子醒來時,烏龜已經領先它5000米,兔子奮起直追,當烏龜到達終點時,兔子仍落后100米,那么兔子睡覺期間烏龜跑了多少米?【分析與解答】 10000-(10000-100)÷5=8020 (米)
(本訓練題適用五年級學生)
小學數學思維訓練“十佳”題(3)
1、分數3/71的分子和分母同時加上一個相同的數,使分數變成1/5。問:這個加上的數是多少?(類比轉化法)【分析與解答】本題的要求是要我們求分子和分母同加上什么數,使分數的分母是分子的5倍。因為分子和分母不管加上什么數,它們的差71—3=68是不變的,所以,根據這一特點,我們一定會想起本題和年齡問題相類似。例如,兒子今年6歲,父親33歲,問幾年以后父親的年齡正好是兒子的4倍?父親與兒子的年齡差是27歲,這個差是不變的。幾年后父親的年齡是兒子的4倍,27歲相當于幾年后兒子年齡的(4—1=)3倍。用除法就可以求出:(33—6)÷(4—1)=9歲,9—6=3年,也就是3年后父親的年齡是兒子的4倍。
同理,本題中分母與分子的差68相當于新分子的(5—1=)4倍,用除法可求出新分子,進而再求出分子和分母同加上的是什么數。(71—3)÷(5—1)—3=14,即分子與分母同時加上14,可以使分數變成1/5。
2、某商品76件,出售給33位顧客,每位最多買3件,買1件按定價,買2件降價10%,買3件降價20%。最后結算,平均每件恰好按原價的85%出售,那么買3件的顧客有多少人?(類比轉化法)【分析與解答】題目已給出平均數85%,可以作為比較的基準。1人買3件少5%×3;1人買2件多5%×2;1人買1件多15%×1。1人買3件與1人買1件組成A組,即按1:1的比例;2人買3件與3人買2件組成B組,即按2;3的比例。A組是2人買4件,每人平均買2件;B組是5人買12件,每人平均買2.4件。
現在已經建立了一個雞兔同籠模型的問題:總腳數76,總只數33,兔腳數2.4,雞腳數2。B組人數是(76—2×33)÷(2.4—2)=25人,其中買3件的有25÷(2+3)×2=10人,買2件的有25÷(2+3)×3=15人;A組人數是33—25=8人,其中買3件的有4人,買1件的有4人。也就是說買3件的一共有10+4=14人。
3、兩人輪流從1,2,3,……,9這9個數字中取數。每次取1個,誰先取的數中有3個數的和為15就算贏家。如果第1個人取的數是5,那么第2個人應該取幾才能使自己立于不敗之地?(類比轉化法)【分析與解答】這個問題實際上是“井字棋”游戲,乙的對策如果不對,會導致失敗。本題條件中的“和為15”,使我們聯想到“三階幻方”,它的每行、每列及對角線的和都是15。故本題等價于甲乙二人輪流將黑白二色棋子放入九宮格中,哪一方放入的棋子先成一行(橫行、豎行和斜行)者為勝。甲先占了中間一格,乙應選哪一格才能保證自己不敗?
假設乙選擇邊上的位置,比如選3,則甲選4,乙只好選6。甲再選2,這時8、9這兩個位置乙只能選一個,甲必得其一,這樣甲就必勝無疑了。
當甲選5時,乙應選九宮格中位角上的數字,即應選2、4、6、8中的一個,才能使自己立于不敗之地。
4、21個球隊用淘汰制決定冠軍,總共要賽多少場?(逆推法)【分析與解答】淘汰制就是每兩個隊比賽一場淘汰一個隊,依此類推,賽到最后一對,勝利者就是冠軍。解答此題的一般是順推法,比較復雜,如果用逆推法就簡單、巧妙得多。
因為淘汰一個隊要賽1場,總共是21個隊,而獲得冠軍的只有1個隊,也就是說要淘汰20個隊,總共要賽20場。
5、一份試卷共25道題。每一道題給出4個答案,其中只有一個正確。要求考生把正確的選出來,每選對一題得4分,不選或錯選扣1分。如果一個學生得90分,那么他做對了幾道題?(逆推法)【分析與解答】此題按正向思維的方法解,很難,要不就用假設法。如果用逆推法就簡單、巧妙得多。因為選錯或不選扣1分,與做對相比,損失5分,得90分的人被扣了10分,這就是選錯或不選的有2道題,所以選對了23題。
6、一年級和六年級共100人摘了100千克茶葉,六年級每人摘3千克,一年級每3人摘1千克,問一年級和六年級各有多少人?(分組法)【分析與解答】學生一般用假設法來解答這類題。如果用分組法解答此題就更簡單、更容易理解。
因為六年級1人摘3千克,一年級3人摘1千克,所以把六年級的1人和一年級的3人分為一組,這4人可以摘茶葉4千克,100千克里有幾個4千克,就有幾組學生,有幾組就有幾名六年級的學生。100÷(3+1)=25人,100—25=75人。
7、甲乙二人做換棋子游戲,甲有100個棋子,乙有20個棋子。如果甲每次給乙5個棋子,乙再還給甲3個棋子,那么按照這樣的方法連續調換多少次,乙的棋子是甲的3倍?(抓不變量)【分析與解答】此題如果我們按照甲的棋子每次減少(5—3)個,乙的棋子每次增加(5—3)個,一步一步地推算,解答起來就很麻煩。如果能抓住“和不變”進行思考,問題就簡單了。當“乙的棋子是甲的3倍”時,則兩人共有的棋子(100+20)個就相當于甲這時所有棋子的(3+1)倍。(100+20)÷(3+1)=30個,(100—30)÷(5—3)=35次。
8、龜兔進行10000米賽跑,兔子的速度是龜的速度的5倍,當它們從起點一起出發后,龜不停地跑,兔子跑到某一地點開始睡覺,兔子醒來時,龜已經領先它5000米。兔子奮起直追,但龜到達終點時,兔子仍落后100米,那么兔子睡覺期間龜跑了多少米?(靈感思維)【分析與解答1】假定兔子不睡覺(這是巧妙之處),當龜跑完全程10000米時,兔子應跑10000×5=50000米,但實際上只跑了10000—100=9900米,少跑了50000—9900=40100米,這40100米正是兔子睡覺所耽誤的路程。因此在兔子睡覺期間龜跑了40100÷5=8020米。
【分析與解答2】假定兔子一次性跑到離終點100米處在睡覺(這是巧妙之處),此時兔子跑了10000—100=9900米,龜跑了9900÷5=1980米,剩下10000—1980=8020米,這正是在兔子睡覺期間龜跑的路程。我們不難發現,題目中的條件“5000米”是多余的。
9、把14拆成幾個自然數的和,再求出這些數的乘積,如何拆可使乘積最大?(極端思維)【分析與解答】十分明顯,這樣的數是很多的,我們不可能也沒有必要一一找,如果用極端思維,情況就變得十分簡單了。首先把14這個數推向最大的一端,拆的個數要盡可能多,多一個可多乘一次,接著把加數推向最小一端:加數不宜超過4,比如5拆成2和3,則2×3>5,這就說明加數大于4的,要盡量拆小;但不應出現1,因為1與任何數的乘積仍為原數;另外在所拆的數中,2的個數不能多于2,因為2×2×2<3×3。
這樣14應盡可能拆成3,因為4×3=12,所以14拆成了3、3、3、3、2時,這些數的乘積最大,其乘積為3×3×3×3×2=162。
10、有一天,某商店估計將進貨單價為90元的某商品按100元售出后,能賣出500個。已知這種商品每個漲價1元,其銷售量就減少10個,為了使這一天能賺得更多利潤,售價應定為每個多少元?(極端思維)【分析與解答】這道題目的數量關系比較復雜,而題目所給的條件不夠充分,若用一般的方法去分析解答,看來比較困難。我們不妨抓住題目中的“漲價”和“銷量減少”這兩個極端,問題就容易解答了。
因為按每個100元出售,能賣出500個,每個漲價1元,其銷量減少10個,所以,這種商品是按單價90元進貨,共進了600個。現把600個商品按每份10個,可分成60份,因每個漲價1元,銷售就減少1份(即10個);相反,每個減少1元,銷售就增加1份。所以,每個漲價的錢數與銷售的份數之和是不變的(為60),根據等周長長方形面積最大原理可知,當把60分為兩個30時,即每個漲價30元,賣出30份,此時有最大利潤。因此,每個售價定為90+30=120元時,這一天能獲得最大利潤。
小學數學思維訓練“十佳”題(4)
1、猜猜是幾?一個三位數,寫在一張紙上,倒過來看是正著看的1.5倍,正著看是倒過來看的2/3,這個三位數是幾?
【分析與解答】這個三位數是666。其實,只要你稍加思索,就可以想出來了。這道題如果要求找一個一位數,那就是6;找一個兩位數,則是66;找一個四位數,則是6666,依此類推。
2、一筐蘋果入冬前,媽媽買來了一筐蘋果,清理時,發現這筐蘋果2個、2個地數,余1個;3個、3個地數,余2個;4個、4個地數,余3個;5個、5個地數,余4個;6個、6個地數,余5個。你知道這筐蘋果至少有多少個嗎?
【分析與解答】根據題目條件,可以知道,這筐蘋果的個數加1,就恰好是2、3、4、5、6的公倍數。而題目要求“至少有多少個”,所以,蘋果的個數應該是2、3、4、5、6的最小公倍數減去1。[2,3,4,5,6]=60 60-1=59 即這筐蘋果至少有59個。
3、有這樣的數嗎?小明異想天開地提出:“世界上應該存在這樣兩個數,它們的積與它們的差相等。”他的話音剛落,就引起了同學們的哄堂大笑,大家都覺得這是不可能的。但是,世界上有些事情往往產生于一些怪想法。小明的想法,后來竟被同學們討論證實了。你能找到這樣的兩個數嗎?告訴你,這樣的數還不止一對呢!
【分析與解答】下面舉出幾個兩數的積等于兩數的差的實例:

同學們,你可再試著找一些。
4、
關鍵在于觀察你在數學課上學了不少幾何圖形的知識,掌握了不少平面圖形的求面積公式。但是有許多組合面積的計算,單靠這些知識是遠遠不夠的,它更需要對組合圖形的觀察能力。下面就是一道考查你的觀察能力的題目。試試看,你能很快做出來嗎?
已知圖內各圓相切,小圓半徑為1,求陰影部分的面積。
 【分析與解答】
【分析與解答】把半圓展開成整圓。可看出
除小半圓外的陰影面積是大圓減掉6個小圓后的1/6,再加上小半圓面積即可。
5、
擴大魚池養魚專業戶張強,去年承包了一個叫“金三角”的魚池(如下圖),喜獲豐收。為了進一步增產,決定把魚池擴大。但有這樣的要求:①擴大后的魚池必須仍是三角形,保持“金三角”魚池的稱號;②擴大后的魚池面積是原面積的4倍;③原魚池的三個角上栽的3棵大柳樹不能移動。你能替張強設計一個施工草圖嗎?
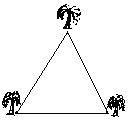 【分析與解答】
【分析與解答】金三角”一定是一個很特殊的三角形。擴大后的面積是原面積的4倍,則還差三個“金三角”,拿三個“金三角”去原“金三角”拼擺,即可做到柳樹不會移動,而且面積擴大4倍,而且形狀還是“金三角”。自然就能發現這個“金三角”肯定就是“等邊三角形”。
6、
五個少年五個少年,依次相差一歲,在1994年共同發奮學習,到公元2018年時,他們都在科學上做出了很大貢獻。那時他們的年齡也增長了,他們五人在公元2018年的年齡之和正好是1994年的年齡之和的3倍。問在1994年時他們的年齡各是多少?
【分析與解答】設年齡為中間數的一個少年在1994年是x歲,則其余四人的年齡分別為x-2歲、x-1歲、x+1歲、x+2歲。
在1994年五人年齡之和為(x-2)+(x-1)+x+(x+1)+(x+2)=5x
2018年五人年齡之和為5x+24×5=5(x+24)
因為這五個少年2018年的年齡之和是1994年年齡之和的3倍,所以
5(x+24)=3×5x,解得x=12
因此,這五個少年的年齡分別為 10歲、11歲、12歲、13歲和 14歲。
7、一本書的頁數我們知道印刷廠的排版工人在排版時,一個數字要用一個鉛字。例如15,就要用2個鉛字;158,就要用3個鉛字。現在知道有一本書在排版時,光是排出所有的頁數就用了6869個鉛字,你知道這本書共有多少頁嗎?(封面、封底、扉頁不算在內)
【分析與解答】仔細分析一下,頁數可分為一位數、兩位數、三位數、……。一位數有9個,使用1×9=9個鉛字;兩位數有(99-9)個,使用2×90=180個鉛字;三位數有(999-90-9)個,使用3×900=2700個鉛字;依此類推。
我們再判斷一下這本書的頁數用到了幾位數。因為從1到999共需用9+2×90+3×900=2889個鉛字,從1到9999共需用9+2×90+3×900+4×9000=38889個鉛字,而2889<6869<38889,所以這本書的頁數用到四位數。
排滿三位數的頁數共用了2889個鉛字,排四位數使用的鉛字應有6869-2889=3980(個),那么四位數的頁數共有3980÷4=995(頁)。因此這本書共有999+995=1994(頁)。
8、
畫一畫下面這些圖形你能一筆畫出來嗎?(不重復畫)
 【分析與解答】
【分析與解答】一筆畫需要解決兩個關鍵問題。一個是這幅圖能不能一筆畫?另一個是,若能一筆畫,應該怎樣畫?對于這兩個問題,數學家歐拉在1736年研究了“哥尼斯堡七橋”的問題后,做了相當出色的回答。他指出,如果一幅圖是由點和線連接組成,那么與奇數條線相連的點叫“奇點”;與偶數條線相連的點叫“偶點”。
例如,在圖17中,B為奇點,A和C為偶點。
如果一幅圖的奇點的個數是0或是2,這幅圖可以一筆畫,否則不能一筆畫。這是對第一個問題的回答。歐拉又告訴我們,如果一幅圖中的點全是偶點,那么,你可以從任意一個點開始畫,最后還回到這一點;如果圖中只有兩個奇點,那么必須從一個奇點開始畫,并結束于另一個奇點。
本題的4幅圖,其中圖(1)、(4)各有兩個奇點,圖(2)、(3)的奇點個數為0。因此這4幅圖都可一筆畫。畫法請參看圖

9、
越減越多同學們對這樣的問題可能并不陌生:“一個長方形被切去1個角,還剩幾個角?”這種題的最大特點是答案不唯一,要根據去掉的這個角的不同情況來確定“剩角”的多少。
以下3幅示意圖,表明了3種不同情況的3種不同答案。其中第3種情況最有趣,長方形原有4個角,切去了1個角,反而多了1個角,出現了越減越多的情況。下面一道題的思考方法與上題類似,看你能否正確回答。

“一個正方體,鋸掉一個角,還剩幾個角?”請注意,這里的“角”是立體的“角”,它不同于平面上的角。
【分析與解答】鋸掉角的情況有4種,因此剩角的答案也有4種(如14圖所示)。
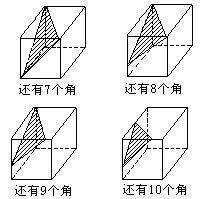
10、
河邊洗碗有一名婦女在河邊洗刷一大摞碗,一個過路人問她:“怎么刷這么多碗?”她回答:“家里來客人了。”過路人又問:“家里來了多少客人?”婦女笑著答道:“2個人給一碗飯,3個人給一碗雞蛋羹,4個人給一碗肉,一共要用65只碗,你算算我們家來了多少客人。”
【分析與解答】題目給出了碗的總數,以及客人和碗的關系。如果能求出每人占用多少只碗,那么就可以求出客人的數目了。

小學數學思維訓練“十佳”題(5)
1、計算:(1+2+3+4)×(2+3+4+5)-(1+2+3+4+5)×(2+3+4)[分析與解答]:注意到這幾個分數多次出現,我們把第一個括號里的(
2+
3+
4)看成是一個數a, 把第二個括號里的(
2+
3+
4+
5)看成是一個數b,那么第三個括號里是(1+b), 第四個括號里就是a.
解:設
2+
3+
4=a
2+
3+
4+
5=b
原式=(1+a)×b-(1+b)×a =b- a=
52、下邊是一個殘缺的乘法豎式,那么乘積是多少?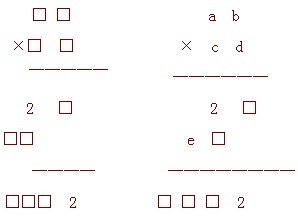
[分析與解答]:如右式。顯然,e=9,d≤2。如果d=1,則a=b=2,此時e不可能等于9,矛盾,所以d=2,a=b=1。因為e=9,所以c=9,得到11×92=1012
3、小王、小張、小李在一起,一位是工人,一位是農民,一位是戰士。現在知道小李比戰士年齡大,小王和農民不同歲,農民比小張年齡小。那么誰是工人?誰是農民?誰是戰士?[分析與解答]:
由“小李比戰士年齡大”,說明小李不是戰士,在小李的戰士格子上打×;由“農民比小張年齡小”,說明小張不是農民,在小張的農民格子上打×;又由“小王和農民不同歲”,說明小王不是農民,在小王的農民格子上打×。觀察知道小李是農民,在小李的農民格子上打√。他們的年齡從大到小的順序是小張>農民=小李>戰士,因此,小王是戰士,小張是工人,小李是農民。
4,已知正方形ABCD的邊長為10厘米,過它的四個頂點作一個大圓,過它的各邊中點作一個小圓,再將對邊中點用直線連接起來得下圖。那么圖中陰影部分的總面積等于多少平方厘米?(注π取3.14)
[分析與解答]:如右圖,原題陰影部分相當于該圖的陰影部分的一半。小圓半徑為10÷2=5(厘米),大圓半徑的平方是(5
2+5
2),因此,所求陰影部分的總面積為[(5
2+5
2)×π-5
2π]÷2=39.25(平方厘米)
5、在中國古代算書《張丘建算經》中有一道題:已知小雞一元錢三只,母雞三元錢一只,公雞五元錢一只。現在用一百元錢買一百只雞。問:這一百只雞中,小雞、母雞、公雞各多少只?(每種雞都須買)[分析與解答]:解:設買小雞x只,母雞y只,公雞z只。
X+y+z=100 (1)
3x+3y+5z=100 (2)
(2)×3-(1)得8y+14z=200 4y+7z=100 Y=25-
4z
當z=4時,y=18,x=78; 當z=8時,y=11,x=81; 當z=12時,y=4,x=84;
答:買小雞、母雞、公雞78只、18只、4只;或81只、11只、8只;或84只、4只、12只。
6、兄弟四人一起去買一臺電視機。老大帶的錢是另外三個人所帶錢總數的一半,老二帶的錢是另外三個人所帶錢總數的3,老三帶的錢是另外三個人所帶錢總數的4,老四帶了910元。那么這臺電視機需要多少元?[分析與解答]:先統一單位“1”,再列式計算。例如根據“老大帶的錢是另外三個人所帶錢總數的一半”,把另外三個人所帶錢總數看著單位“1”,則老大帶的錢是四個人所帶錢總數的
2÷(1+
2)=
3 , 910÷(1-
3-
4-
5)=4200(元)
7,某工程隊先由甲單獨做63天,再由乙單獨做28天即可完成。如果由甲乙兩人合作,需48天完成。現在甲先單獨做42天,然后再由乙來單獨完成,那么還需要做多少天?[分析與解答]:思路一:由題目條件可知,甲做15天的工作量相當于乙做20天的工作量,也就是甲的工效是乙的工效的
3倍。由此可推出甲的工效為
7,乙的工效為
7。這樣,甲單獨完成工程需48÷
7=84(天),乙單獨完成工程需48÷
7=112(天)。現甲做了42天,完成了全工程的
2,剩下的
2由乙完成,那么乙需
2÷
112=56(天)。
思路二:把“先由甲單獨做63天,再由乙單獨做28天即可完成”轉化為“先由甲單獨做63-28=35天,再由甲乙合做28天即可完成”。 由此可推出甲的工效為(1-
48×28)÷(63-28)=
84,乙的工效為
48-
84=
112。現在甲先單獨做42天,然后再由乙來單獨完成,那么還需要做的天數是(1-
84×42)÷
112=56(天)。
8,牧場上牧草勻速生長。27頭牛6天吃完;23頭牛9天吃完。如果一群牛12天吃完這片牧草,這群牛有幾頭?[分析與解答]:解:設每頭牛每天吃草量為1。
每天生長的草量:(23×9-27×6)÷(9-6)=15
原有草量: 27×6-15×6=72
這群牛的頭數:(72+15×12)÷12=21(頭)
9、蘇步青教授是我國著名的數學家,他小時侯,一次在電車上,碰到了一位有名的外國數學家,這位外國數學家出了一道題目讓他做。題目是:甲乙兩人同時從兩地出發,相向而行,距離是100千米。甲每小時走6千米,乙每小時走4千米,甲帶著一只狗,狗每小時跑10千米,這只狗同甲一道出發,碰到乙的時侯,它又掉頭朝甲這邊跑,碰到甲的時候又往乙那邊跑,……直到兩人相遇。問這只狗一共跑了多少千米?[分析與解答]不難發現,不論狗在甲乙兩人間跑了多少個來回,狗走的路程所用的總時間等于甲、乙兩人相遇所用的時間。所以,甲、乙兩人相遇所用的時間是100÷(6+4)=10(小時),狗一共跑的路程是10×10=100(千米)
10,俄羅斯作家托爾斯泰曾提出過一道十分有趣的數學題:有一組割草人要完成大小兩塊草地的割草任務。已知大塊面積是小塊的兩倍。上午全組人集中在大塊草地,下午一半人留在大草地,另一半人轉入小草地割草,傍晚收工時,大草地全部割完,小草地剩下的任務剛好第二天由一個人用一天的時間完成。請問這割草組總人數是多少?[分析與解答]:解:設這割草組有x人。
從整體上看,大小兩塊草地需要(x+1)人割一天。已知大塊的面積是小塊的兩倍,那么小塊草地需要
3(x+1)人割一天。由題意知小塊草地需要
2x人割
2天后,剩下的任務剛好第二天由一個人用一天的時間完成,即小塊草地需要(
4x+1)人割一天。
列方程得
3(x+1)=
4x+1 解之得x=8
答:這割草組有8人。
小學數學思維訓練“十佳”題(6)
1.小華的爸爸1分鐘可以剪好5只自己的指甲。他在5分鐘內可以剪好幾只自己的指甲。(分析與解答):20只,包括手指甲和腳指甲。
2、8+1=6,這張卡片寫對了,你知道是為什么嗎?(分析與解答):因為把卡片放倒了,9=1+8;
3、小軍說:“我昨天去釣魚,釣了一條無尾魚,兩條無頭的魚,三條半截的魚。你猜我一共釣了幾條魚?”同學們猜猜小軍一共釣了幾條魚?(分析與解答):0條,因為他釣的魚是不存在的;
4、在廣闊的草地上,有一頭牛在吃草。這頭牛一年才吃了草地上一半的草。問,它要把草地上的草全部吃光,需要幾年?(分析與解答):它永遠不會把草吃光,因為草會不斷生長;
5、人帶貓、雞、米過河,船除需要人劃外,至少能載貓、雞、米三者之一,而當人不在場時貓要吃雞,雞要吃米。試設計一個安全過河方案,并使渡船次數盡量減少。 (分析與答案)::
(1)帶雞過去 空手回來
(2)帶貓過去 帶雞回來
(3)帶米過去 空手回來
(4) 帶雞過去
6、打一數學名家:老爺爺參加賽跑(分析與解答):祖沖之
7、猜數學名詞:(1)全部消滅(2)再見吧!媽媽。
(分析與解答):
(1)除盡(2)分母
8、“牛頓問題”:“有一牧場,已知養牛27頭,6天把草吃盡;養牛23頭,9天把草吃盡。如果養牛21頭,那么幾天能把牧場上的草吃盡呢?并且牧場上的草是不斷生長的。” (分析與解答):假設牛每天吃一份草
27頭6天吃 162 份草
23頭9天吃 207 份草
9-6=3 天內草多長了 207-162=45份
草的長速為平均每天 45/3 = 15份
9天內草長了15×9 = 135 份
所以原來的草場為 207 - 135 = 72 份草
如果有 21 頭牛, 每天吃21份草, 而草場每天就長15份草, 所以牛每天吃掉多長出來的草15份和原草場的6份草. 原草場的72份草需要 72/6=12天吃光
9、有只猴子在樹林采了100根香蕉堆成一堆,猴子家離香蕉堆50米,猴子打算把香蕉背會家, 每次最多能背50根,可是猴子嘴饞,每走一米要吃一根香蕉,問猴子最多能背回家幾根香蕉? (分析與解答):先背50根到25米處,這時,吃了25根,還有25根,放下。回頭再背剩下的50根,走到25米處時,又吃了25根,還有25根。再拿起地上的25根,一共50根,繼續往家走,一共25米,要吃25根,還剩25根到家。
10、50名學生做物理.化學兩種實驗.已知物理實驗做得正確的有40人,化學實驗做正確的有31人,兩種實驗都做錯的有4人,問這兩種實驗都做對的有幾人? (分析與解答):設都做對的有x人,則只做對化學的有(31-x)人,只做對物理的有(40-x)人。列等式如下 :50=4+(40-x)+(31-x)+x , x=25 ,所以兩種都對的有25人。
小學數學思維訓練“十佳”題(7)
1、有一列數1、2、3、2、1、2、3、4、3、2、3、4、5、4、3、、、、、、、,這列數中,第2000個數是多少?這2000個數的和是多少?[分析與解答]我們通過觀察可以了現此題的排列規律是:如果我們從第一個數開始,以每5個數為一段,那么各段的第一個和第五個數依次分別為1、2、3、4、5、、、、、、。每段中的5個數的各依次分別為9、14、19、24、、、2004,排成一個公差為5的等差數列。觀察每相鄰兩段的五個數便可發現,后面的五個數分別比前面的五個數多1,一共增加5。解;因為2000*5=400所以第2000個數是400。這2000個數的總和是:(9+2004)乘以400除以某2=402600
2、某鐘面的指針在2點整,再過多少分釧時針和分針第二次重合?[分析與解答]這個問題實際上就是行程中的追及問題。當用時針一小時轉動的一格作為路程的單位時,分針的速度為每分鐘1/5格,時針的速度為每分釧1/60格,即時針速度是分針速度的1/12,然后運用追及問題的有關知識來解答。解:因為釧面上的指針指在2點整,則此時時針與分針起始的位置相距2個格,當首次重合時分針比時針多走2格,所以第二次重合時,分針應比時針多走一圈,即分針比時針共多走14格,則丙針第二次重合的時間為;14除以(1/5-1/60)=76+4/11分。
3、某數被5除余2,被6除少2,被7除少3。這個數最小是多少?[分析與解答]將題目加以轉化,被6除少2,即被6除余4,被7除少3即被7除余4。先求出符合兩個條件的最小數6乘7加4等于46。再在46的基礎上逐一加上6和7的最小公倍數42總能滿足兩個條件,直至符合第一個條件為止。解:6乘7加4等于46 46+42=88(被5除余3舍去)46加42乘2等于130(被5除無余數,舍去)46加42乘3等于172(被5除余2,符合條件)。
4、某商店從外地購進360個玻璃制品,運輸時抽壞了40個,剩下的按進價的117%售出,商店可仍可盈利百分之幾?[分析與解答]求盈利百分之幾,也就是求得利潤占成本的百分數,即用總售價與成本價之差除以成本價,但每個玻璃制品的成本價不知道,可以設為A元再計算。則每個偽價為1、17A元。解;1、17A乘以(360-40)-360A的結果除以360A 等于4%。
5、甲丙兩個倉庫存放的貨物重量比是4比3,把甲倉庫貨物的1/3運到丙倉庫,這時珍倉庫貨物比甲倉庫多100噸。甲倉庫原有貨物多少噸?[分析與解答]甲丙兩倉庫貨物重量比是4比3,則丙倉庫的重量占甲倉庫的3/4,把甲倉庫的1/3運到丙倉庫后,則甲倉庫剩2/3,丙倉庫有甲倉庫的3/4+1/3,丙倉庫比甲倉庫多甲倉庫的3/4+1/3-(1-1/3),即多100噸,可列式求出甲倉庫原有貨物的重量。解:100除以[3/4+1/3-(1-1/3)]=240噸。
6、要想得到濃度為8%的鹽水若干千克,應往40千克濃度為20%的鹽水中加多少千克水?[分析與解答]學度為20%降低為8%,即鹽水由咸變淡,屬于稀釋類問題,鹽水稀釋后,濃度發生了變化,溶劑水發生了變化,鹽水也發生了變公,但上于稀釋是加進水所造成的,鹽水中的含鹽量并未姓變化,這是一個不變量,根據這個條件可以列方程解答。充應加水A 千克。40乘20%-(40+A)乘8% A等于60所以加水60千克。
7、森林中,獵狗發現前方20米處有一只奔跑的野兔,立即追去,獵狗步子大,它跑5步的路程式,兔 子要跑9步,但兔子動作快,獵狗2步的時間,兔子卻能跑3步,獵狗跑出多遠才能追上野兔?[分析與解答]求這道題的關鍵是要知道在相同的時間內,獵狗與兔子跑的路程式之比。如果把獵狗跑5步的路程式看作單位1,則獵狗每步長1/5,兔子每步長1/9。在相同時間內,獵狗可以跑2步,兔子可以跑3步。在相同的進間內,獵狗 與兔子跑的路程之比是1/5乘2比1/9乘3等于6比5 ,再根據公分數應用題求出獵狗的路程。解,獵狗與野兔在相同的時間內跑的路程比是:(1/5乘2):(1/9乘3)=2/5:1/3=6:5所以20除以(1-5/6)=120米。
8、A、B 兩個同學數學競賽扮數之比是5:4。如果A少得15分,而B多得23分,則他們兩面三刀人的得分比為15:19。問A 、B兩人共得多少分?[分析與解答]設A 變化前的分數為X 分,則B 變化前的分數為4/5XWV ,P SU A變化后的分數是(X-15)分,B 變化后的分數是(4/5+25}分。再通過列比例式求出A 、B各得多少分。解(X-15):(4/5+23)=15:19 X=90
90X(1+4/5)=162,兩人共得162分。
9、一底面周長是3、14分米的賀柱形玻璃杯內裝有一些水,恰恰相反好占杯子容量的2/5。將兩面三刀個同樣大小的雞蛋放入杯中,浸沒在水里,這時水面上升8、2厘米,剛好與杯口平齊。求一個雞蛋的體積和杯子的容積。[分析與解答]根據題意,當兩個雞蛋放入杯中,杯中水面上升8、2厘米,上升的這一問好分水的體積就是兩個雞蛋的體積,這樣可求一個雞蛋的體積,而上升的這一部分水的體積剛好占杯子容量的1-2/5=3/5,所以可求出杯子的容積。解一個雞蛋的體積3。14X(3。14除以/3。14乘以2)的平方乘方0。82除以2等于0。32185立方分米等于322立方厘米322乘方2除以3/5=644除3/5=1073立方厘米。
10、實驗室里有一只特別的鐘,一圈共有20格。每過7分鐘,指針跳一次,每跳一次就要跳過9格。今天早晨8時整,指針恰好從0跳到9時,昨天晚上8時整的時候針指著幾?[分析與解題]要求出題目中的問題,必須知道從昨天晚上8時到今天早上8時這段時間內,這只特別的鐘跳了多少次,共跳了多少格。解從昨天晚上8時到今天早上8時共經過60X12=720分720除7=102、、、、、、、6這段時間跳102次,共跳了9X102=918格918除20=45、、、、、、1820-18=2昨天晚上進指針指著2。
小學數學思維訓練“十佳”題(8)
1、小明原來有圖書35本,后來,爸爸買給他18本,小姨又送給他12本。小明的圖書比原來增加了多少本?[分析與解答] 一般解法:①爸爸買給他18本后小明有圖書多少本?35+18=53(本);②小姨送給他12本后小明有圖書多少本?53+12=65(本);③小明的圖書比原來增加了多少本?65-35=30(本)。
這道應用題用一般方法解答,既麻煩又費時。可運用方法簡便的“華羅庚法”解,只需一兩步就可以解答出來。華羅庚法:小明的圖書比原來增加的本數就等于爸爸和小姨送給他圖書的本數的和。18+12=30(本)
2、比較下面兩個積的大小A○B。A=987654321×123456789 B=987654322×123456788
[分析與解答]由“分配律”想:A=987654321×123456788+987654321,B=987654321×123456788+123456788。因為 987654321>123456788,所以 A>B。 由“兩數的和一定時,兩數的差越小積越大,相等時積最大”想:因為 987654321+123456789=987654322+123456788,而 987654321—123456789<987654322—123456788,前差比后差小2。知 A>B。
3、如果現在的時間是11時11分鐘,那么再過143999999993分鐘是幾時幾分鐘呢?你能用簡單的方法計算嗎? [分析與解答]初看起來,要想知道最后結果,必須先求出143999999993分鐘是多少小時,再求出是多少天零多少小時,才能推算出具體時間。可這樣做太麻煩了,像下面這樣就簡單多了。143999999993+7=144000000000(分);而1天是1440分鐘,所以144000000000H1440=100000000(天)。因為加上了7分鐘,所以最后結果要減去7分鐘。因此題中所求的時間是11時零4分鐘。這道題目從表面上看比較麻煩,需要進行大量的計算,并且在計算的過程中稍一粗心就會出現錯誤,當發現錯誤再回過頭去卻很難找出錯誤在哪里,無奈又得從頭算起。怎樣才能避免大量的運算,使計算迅速而簡便呢?這就是要想方設法尋求簡單的計算方法。
4、看誰能最快指出下面四道題中哪兩道的計算結果相同。①48×6÷4×7×4÷8 ②128×9+72×9
③48×4÷6×7×6÷8×8 ④342×9-9×142
[分析與解答]題目要我們找出哪兩題計算結果相同,那我們就可以找一找哪兩題形式相同,然后再仔細比較一下,它們在計算結果上會有什么不同的地方,這樣就可以初步估算出計算結果是否相同了。例如,第①、③兩題,都是48與4、6、7、8幾個數相乘、除,我們把這兩題中相同的數以及相同的運算符號劃去。 ①48×6÷4×7×4÷8 ③48×4÷6×7×6÷8×8;結果第①題只剩下“÷4”,第③題剩下“÷6”和“×8”可見這兩道題的計算結果是不相同的。而第②題和第④題都是9的倍數的計算,第②題是128個9加上72個9,一共是200個9;第④題是342個9減142個9,得200個9。所以這兩道題計算結果是相同的。”
5、今有甲乙丙丁四人在晚上都要從橋的左邊到右邊。此橋一次最多只能走兩人,而且只有一支手電筒,過橋是一定要用手電筒。四人過橋最快所需時間如下為:甲:2 分鐘;乙:3 分鐘;丙:8 分鐘;丁 10分鐘。走的快的人要等走的慢的人,請問如何走法才能在 21 分鐘讓所有的人都過橋? [分析與解答]先是甲和乙一起過橋,然后將乙留在對岸,甲獨自返回。甲返回后將手電筒交給丙和丁,讓丙和丁一起過橋,丙和丁到達對岸后,將手電筒交給乙,讓乙將手電筒帶回,最后甲和乙再次一起過橋。則所需時間為:3+2+10+3+3=21分鐘。
6、六位數□4321□能被4321整除,這個六位數是多少? [分析與解答]這道題目初看起來似乎難度較大。如果我們采用“假設──計算──排錯──驗證”的方法,問題就會很快得解。假設六位數為943219,那么943219÷4321=218…1241,由于余數大于9,所以不合題意。假設六位數為843219,則有843219÷4321=195…64,余數大于9,也不合題意。假設六位數為743219,則有743219÷4321=172…7,余數小于9,由此可見符合條件的六位數為743219-7=743212。當六位數的首位數分別為6、5、4、3、2、l時,經計算可知均不合題意。綜上分析可知,要求的六位數只能為743212。
7、前進小學8個班去幫助農民摘豆角,每個班摘豆角的重量分別是:55千克、50千克、48千克、54千克、49千克、53千克、54千克、53千克。問平均每班摘豆角多少千克?(看誰算得快) [分析與解答] 求平均數有個竅門,就是先在這些數中確定一個基準數。這道題就是以50為基準數。然后把5個班分別比基準數多出的千克數加起來,并從中減去剩下那2個班比基準數少的千克數,所得的數除以8,商再加上基準數,就是所求平均數。這種方法我們可以給一個名字叫做“減少加多法”。做的時候可以這樣:先選好基準數50,然后從前往后看,多的數前寫上加,少的數前寫上減,也就是:5+0-2+4-l+3+4+3=16;16÷8=2;50+2=52(千克)
8、某公司將3875元獎金給3名優秀員工,第一名比第二名多得250元,第二名比第三名多得125元,這三名優秀員工各得多少元? [分析與解答] 設第三名為C,第二名為C+125,第一名為C+125+250,三個人加起來為3C+500=3875。可得C=1125,這是第三名的。第二名是C+125,即1125+125=1250;第一名是C+125+250,即1125+125+250 =1500。
9、籃子里有四個蘋果,由四個小孩子平均分,到最后,籃子里還有一個蘋果。請問:他們是怎樣分的? [分析與解答]這個問題的答案只能是:四個小孩一人一個。這個答案許多人可能摸不著頭腦:不是說四個孩子平均分四個蘋果嗎?那籃子里剩下的一個怎么解釋呢?首先,題目中并沒有 “剩下”的字眼;其次,那三個小孩子拿了應得的一份,最后一份當然是最后一個孩子的。至于他把蘋果留在籃子里或者拿在手上,這并沒有什么區別。
10、某店來了三位顧客,急于要買餅趕火車,限定時間不能超過16分鐘。幾個廚師都說無能為力,因為要烙熟一個餅的兩面各需要五分鐘,一口鍋一次可放兩個餅,那么烙熟三個餅就得2O分鐘。這時來了廚師老李,他說動足腦筋只要15分鐘就行了。你知道該怎么來烙?[分析與解答]首先把兩個餅一齊放到鍋里烙5分鐘,然后把其中任何一塊餅反轉過來烙另一面,同時把另外一個餅拿走,并且把第三個餅放到鍋上,跟已經烙了5分鐘的那個餅一齊再烙5分鐘。5分鐘過后(這時已經過了10分鐘),把兩面都烙好了的那塊餅拿起,然后將在鍋里的另一塊餅翻轉到另一面繼續烙,同時把起初已烙了一面的那一塊餅放回到鍋里繼續烙另一面。5分鐘過后(這時剛好過了15分鐘),鍋里的那兩塊餅都烙好了。也就是說,那位聰明的廚師,總共只用了15分鐘就把3塊餅全部烙好了!
小學數學思維訓練“十佳”題(9)
一、一個兩位數質數,交換個位與十位上的數字,所得的兩位數仍是質數,寫出這樣的兩位數。[分析與解答]這個題目首先考慮兩位數的兩個數字都是奇數有一個數字是偶數時,交換位置,這個數就不會是質數了。如11、13、17、37、79
二、三筐桔子共重100Kg,一二兩筐重66 6Kg,二、三筐重693Kg求這三筐桔子各重多少千克?[分析與解答]一二兩筐和二三兩筐重量的和減去三筐共重的,得第二筐的重量。
第二筐:66
6+69
3-100=35
2(kg)
第一筐:66
6-35
2=31
3(kg)
第三筐:69
3-35
2=33
6(kg)
三、一只底面是正方形的長方體鐵箱,如果把它的側面展開,正好得到一個邊長是40cm的正方形,求這只鐵箱的容積是多少升?[分析與解答]側面展開得到一個邊長是40cm的正方形,說明底面正方形周長為40cm,則邊長為40÷4=10(cm)。這個長方體的高就是40cm。容積=10×10×40=4000(cm3)=4000(ml)=4(L)
四、38的分數單位是( 8),減去(13)個這樣的分數單位得到最小的質數。[分析與解答]把3
8化成假分數為
8,則分數單位為
8,減去多少個這樣的分數單位得到最小的質數,這需弄清楚最小質數為2,則
8-2=
8,
8中有13個
8五、被減數比減數多40,比差數多35,減數是被減數的(15)。[分析與解答]被減數比減數多40,這就是告訴我們差是40,比差多35這就是告訴我們減數為35,則被減數為40+35=75,減數是被減數的
75=
15。
六、把長1m的長方體木棍截成3段,表面積加20c㎡,這根木棍的體積是(500)cm3。[分析與解答]把木棍截成3段,截了2次,橫截面增加了4個,則橫截面為
20÷4=5(c㎡)
1m=100cm 體積 5×100=500(cm3)
七、一個合數的質因數是10以內所有的質數,這個合數是(210)[分析與解答]10以內所有質數為2、3、5、7.則這個合數為2×3×5×7=210
八、把 5的分子增加6,要使分數的大小不變,它的分母應該怎樣變化?[分析與解答]此題要求出分母的變化,就要知道分子增加6,是擴大了幾倍。 6÷3 =2
分子由3增加6擴大了2倍應是擴大到2﹢1倍,要使分數不變,則分母應為5×3=15。15-5=10.分母增加10。
九、x(x是自然數)它的分數單位是(x)。當x是(8)時,它是最小的假分數,當x大于(8)時它是真分數,當x是(2)時它是最小的合數。[分析與解答]分數單位是把單位“1”平均分成若干份,取其中1份,這里平均分成x份,則它的分數單位是
x,最小的假分數是分子和分母相等則x為8,真分數是分母大于分子,則x大于8時,最小的合數是4則x為2。
十、分母是10的全部最簡真分數的和是(2)[分析與解答]此題一定要審題,分母是10的全部最簡真分數有
10、
10、
10、
10 10+
10+
10+
10=2











